Blog del curso de Termodinamica

Postulado de estado: El estado de un sistema comprensible simple se especifica por completo mediante dos propiedades intensivas independientes.

Presión y Temperatura no pueden ser dos propiedades intensivas

Temperatura y Volumen son dos propiedades intensivas independientes

-          Un ciclo es cuando el estado inicial y el estado final es el mismo

-          Proceso es la trayectoria del Estado 1 al Estado 2

Proceso de cuasi estático o de cuasi equilibrio

             Quasiequilibrium

            Compresión lenta

            Nonquasi-equilibrium

            Compresión Rápida
    

   

-          Cuando la temperatura permanece constante se le llama proceso Isotérmico.

-          Cuando el volumen permanece constante se le llama proceso Isocorico.

-          Cuando la presión permanece constante se le llama proceso Isobático.

Diagrama de P-V(Presion-Volumen)

Un fluido es un conjunto de moléculas que se ordenan aleatoriamente y se mantienen juntas a partir de fuerzas cohesivas débiles y fuerzas que ejercen las paredes de un contenedor.

Presión solo se utiliza para los fluidos

Un fluido es puede ser de forma liquida o gaseoso y este carece de rigidez y elasticidad, este puede tomar la forma de su recipiente.

El colchón de una cama de agua mide 2m de largo y 2m de ancho y 30cm de profundidad.

Encuentre la presión que ejerce el agua sobre el suelo cuando la cama de agua descansa en su posición normal. Suponiendo que toda la superficie inferior de la cama tiene contacto con el suelo.

Presión que se determina en cierto punto se llama presión absoluta

   - Variación de la presión con la profundidad.

 Si el recipiente esta abierto

La presión depende de la densidad del fluido y de la profundidad

Ejemplo 2: La presión absoluta en agua a una profundidad de 5m es de 145 kPa. Determine: a) la presión atmosférica local, b) la presión absoluta a una profundidad de 5m en un líquido cuya densidad relativa es de 0.85 en el mismo lugar.

Ley de Pascal

Un cambio en la presión aplicada a un fluido se transmite sin disminución a todos los puntos del fluido y a las paredes del contenedor.

Ejemplo 3: En un elevador de automóviles en una estación de servicio, el aire comprimido ejerce una fuerza sobre un pequeño pistón que tiene una sección transversal circular y un radio de 5.0cm. Esta presión se transmite mediante un líquido a un pistón que tiene un radio de 15.0cm. ¿Qué fuerza debe ejercer el aire comprimido para elevar un automóvil que pesa 13300N? ¿Que presión de aire produce esta fuerza?

Manómetros (medidores de presión)

El agua en un recipiente se presuriza con aire y la presión se mide por medio de un manómetro de varios fluidos. El recipiente se localiza en una montaña a una altitud de 1400m donde la presión atmosférica es 85.6 kPa. Determine la presión del aire en el recipiente si h₁=0.1m, h₂=0.2m y h₃=0.35m. Tome las densidades del agua, aceite y mercurio iguales a 1000 kg/m³, 850 kg/m³ y 13600 kg/m³, respectivamente.

La presión manométrica en el tanque de la figura es 80kPa. Calcule la altura diferencial h de la columna de mercurio.

Agua dulce y de mar fluyen en líneas paralelas y horizontales orientadas entre si mediante un manómetro de tuvo de doble U. Determine la diferencia de presión entre las dos tuberías considerando la densidad del agua de mar a este punto es de 1035 Kg/m³ ¿Se puede ignorar la columna de aire en el análisis?

Barómetro

El barometro basico se puede utilizar para medir la altura de un edificio. Si las lecturas barometricas en la parte superior y en la base del edificio son 730 y 755mmHg respectivamente, determine la altura del edificio. Tome las densidades del aire y del mercurio como 1.18 kg/m³ y 13600 kg/m³, respectivamente

Ley Cero de la Termodinámica (R. H. Fowler, 1931)

Cuando dos objetos (A y B) están con otro tercero (C) se dice que (A y B) están en equilibrio entre si.

T1>T2
	T1(ºC)	T2(ºC)	ΔT(ºC)	ΔT(ºF)	ΔT(K)	ΔT(R)
	20	15	-5
T(F)	68	59		-9
T(K)	293	288			-5
T(R)	528	519				-9
ΔT(ºF)=1,8ΔT(ºC)
ΔT(R)=1,8ΔT(K)

Una campana de 250mm de diámetro se coloca sobre una superficie plana y el aire se evacua hasta un vacío de 700mmHg. El barómetro local da una lectura de 760mm. Encuentre la presión absoluta dentro de la campana.

P_vacio=(13600 kg/m³)(9.81 m/s²)(0.7 m)=93391.2 Pa

P_atm=(13600 kg/m³)(9.81 m/s²)(0.76 m)=101.39 Pa

P_abs= P_atm- P_vacio=8.006 kPa

P_vacio=700mmHg → 101.325 kPa Mg.

h_Hg=760mm → P_atm==(13600 kg/m³)(9.81 m/s²)(0.76 m)

Calcule la presión en un cilindro de 200mm de diámetro como se muestra en la figura el resorte se comprime 40 cm.

F=-Kx

F=-(-2kN/m)(.4m)=0.8kN

F=mg

F=((40kg)(9.81m/s²)=392.4N

P=F/A

P= (800N+392.4N)/ π(0.1m)² = 37955.27 Pa

F_I-mg-F_S-F_R=0

F_I=P_IA            F_S=P_atmA

P_I= (mg+P_atm+Kx)/A

P_I= [(40kg)(9.81m/s²)(1kN/1000N)]+[(101.325kPa)( π(0.1m)²)]+[(2kN/m)(0.4m)]

                                                           π(0.1m)²

P_I=139kPa

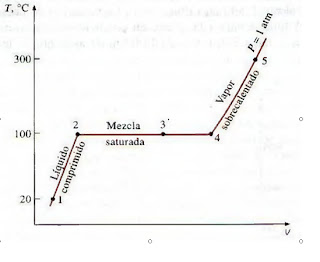
Unidad II: Propiedad de las sustancias puras.

Sustancia pura: tiene 5 fases.

            1.- Líquido Comprimido

           

            2.- Líquido Saturado

            3.- Mezcla Saturada

            4.- Vapor Saturado

            5.- Vapor Sobrecalentado

Ejemplo: Un recipiente rígido condene 50 kg de agua saturada a 90 ºC. Determine la presión en el recipiente y el volumen del mismo.

Liquido saturado

T=90ºC

m=50kg

agua (tabla A-4)

P=P_sat@90ºC=70.183 kPa                      Presión dentro del recipiente

V=V/m

V=V_f@90ºC(m)

V=0.001036 m³/kg(50kg)

V=0.0518m³                                          Volumen

“ESTADO LIQUIDO SATURADO – VAPOR SATURADO”

Ufg = Ug – Uf

Hfg = hg – hf

Hfg= entalpia de vaporización

EJEMPLO: Un recipiente rígido contiene  50kg de agua saturada a 90 ˚C.  Determine la presión en el recipiente y el volumen del mismo.

DATOS:

Agua liquido saturado ….temperatura 90˚C     P = P sat. A 90˚C   = 70.183 kPa

√ = V/m           V =  √ m

                              = (50kg) ( 0.001036 )

                       V = 0.0518

Ejemplo:

V = Vf+ Vp            √ = V/m              V =  √ m                      

  M total √ promedio = mf Df + mg Dg

√ prom. = (m f / m total) vf + X Dg            m f = m total = m g

   √ prom. = ( 1- x) Vf + X Vg

√ prom. = Vf + X Vfg                            gral.

            V = Vf + X V fg                      y = Yf+X Yfg        X = (y – yf/yfg)

Un recipient de 80 lt. contiene 4kg de refrigerante 134a a una presion de 160 kPa . Determine:

a)    La temperatura

b)    La calidad

c)    Entalpia del refrigerante

d)    El volumen que ocupa la  fase de vapor

DATOS:

Fase ¿?   m = 4kg   P = 160 kPa   V = 80 lt.

 √ = V/m         √ = (80 lt ( 0.001      / 1L)) / 4kg      √ = 0.02 

Tabla A-12                          Vf = 0.0007437

a)    -15.60 ˚C                        Vg = 0.12348

b)   X=   (V – Vf) / ( Vfg)     à = ( 0.02 – 0.0007437) / (0.12348 – 0.0007437)

                 X= 0.157

a)    H = hf + x hfg               hfg = 31.21 KJ / Kg

Por  lo tanto h = (31.21) + ( 0.157) (209.90)      X = 0.157  hfg = 209.90 KJ / Kg

      RESULTADO: h = 64.1643 KJ / Kg

b)   Vg = mg √g    à mg = x m total  por lo tanto:

                              Vg = (0.157) (4Kg) (0.12348 m3 / Kg)

                                    = 0.0775 m3   = 77.5 lts.

-VAPOR SOBRECALENTADO-

P < Psat a una T dada

T > Tsat a una P dada

V > Vg a una T o P dada

U > Ug a una T o P dada

h > hg a una T o P dada

-LIQUIDO COMPRIMIDO-

P  > Psat a una T dada

T  < Tsat a una P dada

V < Vf a una P o T dada

u  < Uf a una P o T dada

h < hf a una P o T dada

Aproximada a liquido saturada 

                      Y = Yf a T             Tablas   A - 4  A - 4 E     A - 11   A - 11E

                       Y = V/h

Un vapor a 120 bar tiene un volumen especifico = 0.01721 m3 / Kg , encuentra la Temperatura entalpia y energía interna.

    DATOS:

    Fase ¿?     P 120 bar = 12 MPa      √ = 0.01721 m3 / Kg

Tabla A – 5   Vf a 12MPa  = 0.001526 m3 / Kg

                      Vg a 12MPa = 0.014264 m3 / Kg

V > Vg  >> Vapor sobrecalentado

Ahora … Tabla A – 6

         X = ((0.001566 – 0.001526) / 13 – 12 ) (12.5- 12) + 0.001526

         X = 0.001546 

INTERPOLACION GENERAL

   a1   b1

   a     b                b = [(b2 –b1) / (a2 – a1)] (a - a1) + b1

   a2   b2

por lo tanto…  Vf = 0.001546 m3 / Kg

T = [12846.86536] – [0.01721 – 0.0016138] + 350

T = 363.8 ˚C

P = mg / A   

MODELO DE GAS IDEAL

è Boyle – Mariotte

      V α 1/P ( n, T constante)        donde n = numero de moles

è CHARLES

                   V α T ( n, P ctte)

è AVOGADRO

                   V α nT / P       V = RnT / P

ECUACION del  GAS IDEAL   PV = nRu T       n =  m/M   Ru = ctte universal de los gases

                PV = RT

Ru = ( 1 atm) ( 22.414) / (1 mol) (273.15) =  0.08206 { L * atm / mol * K}

Ru = {…}

è { 0.08206  (L*atm / mol*K)

è  8.114 (Pa*m3/mol*K)

è 62.4  (mm Hg / mol* K)

PV = RT       à P V/M = RT      densidad =  P / RT

1)    n,T        P1V1 = P2 V2

2)    n,P        V1 / T1 = V2 / T2       ””ECUACION  GENERAL DE LOS GASES””

3)    n,V        P1 / T1 = P2 / T2  

                                                                  [(P1 * V1) / T1] = [(P2 * V2) / T2]

Factor de comprensibilidad

Z = PV / RT       z  =  √ / √ ideal             Tr = T / Ter

√r  =  (V presion critica / R tempretatura critica)

Por un tubo pasa el gas de dióxido de carbono a 3 Mpa y 500 K, el flujo constante de 0.4Kmol por segundo, Determine a) las tasas de flujo de volumen y de masa y la densidad del dióxido de carbono en dicho estado. Si el dióxido de carbono se enfria a presión constate al pasar por el tubo de modo que su temperatura baje a 450°K a la salida; determine b) la tasa de flujo volumétrico a la salida del tubo.

P=3Mpa

T=500K

R=.1889KJ/Kg.K

n=0.4Kmol.seg

M=44.01Kg/Kmol

Δ=(300Kpa)/(0.1889Kpa.m³/Kg)(500K)= 31.762m³/Kg

n=m/M    m=nM

m=(0.4Kmol.seg)(44.01Kg/Kmol)

m=17.604Kg.seg

III Primera ley de la termodinámica

3.1 Trabajo de frontera móvil

 

W=FdcosΘ

∫W=FdscosΘ

=Fds

P=F/A

F=PA

∫w =∫Pdv                                                               Isocorico

Wb=∫Pdv

Isobarico

A=BxH=(V₂-V₁)P

Wb=P(V₂-V₁)

V₂>V₁=Wb>0

               ↓

          + el sistema realiza trabajo.

V₁>V₂=Wb<0   → - Se realizo trabajo sobre el sistema.

Ejemplo:

Al principio un dispositivo de cilindro embolo contiene .4m³ de aire a 100 Kpa y 80°C. se comprime el aire a 0.3m³ de tal manera que la temperatura dentro del cilindro permanece constante. Determine el trabajo hecho durante este proceso.

→ V₂=0.1m³

Wb=∫Pdv

P=F(V)

Aire como gas ideal

PV=NRuT

P=(nRuT)/V

Wb=∫nRuT dv/v

Wb=nRuT Ln V|V₂ - V₁

n=(PV₂) /RuT

(P₁V RuT)/RuT, Ln (V₂/V₁)

Wb={100KPa}{0.4m³} Ln (0.1m³/0.4m³)  KJ

Wb= -55.45KJ.

CALOR

                           T°

Q                     m

                      Material, calor especifico (capacidad para amacenar entre mayor es peor conductor)

Q=mc      T° (FINITA)

∫Q=mcdT° (INFINITESIMAL)

Q=mc     T            (J)          n=m/M   m=Nm

C=Q/(m     T)

=J/Kg°C=    J/ Kg°K

Q=n Mc         

       Mc=C      (testado= relacion con molar)

            Capacidad calirifica molar.

Q=nC      T

J/Mol°C  Ó J/Mol°k

¿cambios de fase?                          Calor latente.

Q=±ml (J)

+ agrega calor

-Pierde calor.

Hielo              agua /vapor/ 105°C

-3

Liquido-vapor  Q=mLv                        Vapor-iquido      Q=-mLv

Solido-iquido   Q=mLf                        liquido-solido     Q=-mLf

Una olla gruesa de cobre de 2kg. Incluyendo su tapa esta a una temperatura de 150°C, usted vierte en ella 0.1KG de agua a 25°C y rápidamente tapa la olla para que no escape el vapor. Calcule la temperatura final del vapor y su contenido y determinar la fase liquido gas del agua. Suponga que no se pierde calor al entorno.

Ccobre= 390J/Kg.K                             -Qco=Qagua

Cagua=4190J/Kg/K

Lv= 2.256 x10⁶J/Kg

Suponga que:

i)                    Nada del agu hierve t la temperatura será menor a 100°C

ii)                   Una parte de agua hierve a 100°C

iii)                 El agua hierve y se evapora T=100°C o mas.

i)mal por que T > 100°C

-mcuCcu(T-Tcu)=maca(T-Ta)

(-2Kg)(390J/Kg.K)(T-180) °C= (0.1Kg)(4190J/kg°C)(T-25°C)

-780J/K(T-180)°C=419J/°C(T-25) °C

(-780J/K)/(419J/C)  (T-180)°C= (T-25) °C

1.86(T-180) °C=(T-25) °C

1.86(T-180) °C-(T-25) °C=0

T=106.32°C

-mcuCu (T-Tcu)=maCa(T-Ta)+XmaLv

(-2Kg)(390J/Kg.K)(50°C)= (0.1Kg)(4190J/kg°C)+x(0.1Kg)(2.256X10⁶J/Kg)

39000=31425+2.256X10⁶

X=0.034

Mv=(0.034)(100g)=3.4g

T=100°C

En cierta estufa de gasolina para acampar, 30 de a energía liberada al quemar el combustible calienta el agua de la olla en la estufa. Si calentamos un litro de agua de 20°C a 100°C y evaporamos .25g de ella. ¿cuanta gasolina habremos quemado?. 1 g de gasolina libera 46000 J.

M=1lt.=1Kg.

Q=46000J

T₁=20°C

T₂=100°C

C=4190 J/Kg.k

Q=mc    T=(1kg)(4190J/Kg.k)(100-20) °C

Q=325200J

Liquido vapor

Q=mLv=(.256X10⁶J/Kg)=564000j

1g gasolina=2997333.333J

m=0.0651594 kg

ρ=m/v     V=m/ρ

v=.0651594kg/120kg/m³=9.04941X10⁻⁵m³=.09049=90.5 ml

Balance de energía para sistemas cerrados

EENTRADA-ESALIDA=    ESISTEMA(KJ)           energía interna, energía cinetica, energía potencial.

Transformacion neta de energía y trabajo

Q-W=    U              FORMA FINITA

∫Q-∫W=dv        FORMA INFINITESIMAL

Se condensa isotérmicamente vapor sasturado a 200°C hasta liquido saturado en un dispositivo de cilindro embolo. Calcule el calor transferido y el trabajo efectuado en este proceso en KJ/Kg.

                                                                                                                                                          

                                                                                                               

1                                                                                                               2

Vapor saturado (Vg@200°C=.12721m³/kg)                      liquido saturado( Uf@200°C=.001157m³/kg)

¿Q  y W?

BALANCE DE ENERGIA

Wb-Q=     U

Wb –Q=U₂-U₁

Uf@200°C                   UG@200°C

P₁=P₂=1554.9KPa

Wb=∫Pdv

Wb=Mp(Vf-Vg)

Wb/m=1554.9KPa(.001157-0.12721)m³/Kg

Wb=-196KJ/Kg

Wb-q=U₂-U₁

Q= Wb-u₂+U₁= 196KJ/Kg  -  850.46KJ/Kg  + 2594.2KJ/Kg

1940 KJ/Kg

Un recipiente rigido de 1ft³ contiene refrigerante 134-aoriginalmente a -20°F Y 27.7% de calidad. A continuación se calienta el refrigerante hasta que su temperatura es 100°F calcule la transferencia de calor necesaria para este proceso.

Un dispositivo de cilindro embolo se expande 25g de vapor de agua saturado a una presión constante de 300Kpa. Se enciende un calentador de resistencia eléctrica dentro de cilindro y pasa  una corriente de .2A durante 5 min. Desde una fuente de 120V. al mismo tiempo ocurre una perdida de calor de 3.7 J. determine la temperatura final del vapor.

Un dispositivo que consta de un cilindro embolo contiene inicialmente .5m³ de gas nitrógeno a 400pa y 27°C .dentro del dispositivo se enciende un calentador eléctrico con el cual pasa una corriente de 2 amperes durante 5 minutos, desde una fuente de 120v. el nitrógeno se expande a presión constante y ocurre una perdida de calor de 2800 J durante el proceso determine la temperatura final de nitrógeno.

La salida de potencia de una turbina de vapor adiabatica es 5MWmientras que las condiciones de entrada y salida son como se indica en la figura

a)determine el trabajo hecho por unidad de masa del vapor de agua que fluye por la turbina

b) calcule el flujo masico de vapor

Se tiene una regadera ordinaria donde se mezclan agua caliente a 140°F y fría a 50°F.se desea suministrar una corriente estable de agua caliente a 110°F.determine la relación de los flujos masicos de agua caliente y fría. Suponga que las paredes de calor desde la cámara de mezclado son insignificantes y que el mezclado ocurre a una presión de 20Psia.

Refrigerante 134-a se va a enfriar con agua en un condensador. El refrigerante entra al dispositivo con un flujo masico de 6Kg.m a 1 Mpa y 70°C, y sale a 35°C. e agua de enfriamiento entra a 300Kpa y 15°C y sale a 25°C. sin considerar las caídas de presión determine a)el flujo masico de agua de enfriamiento requerido b) la tasa de transferencia de calor desde el refrigerante hacia el agua.

Balance de masa y energía en sistemas abiertos

Principio de la conservación de la masa

Flujo estacionario este es cuando no cambia con respecto al tiempo

Energia o trabajo de flujo

W_flujo=FL=PAL=PV [kJ]

W_flujo=PV  [kJ/kg]

Energia total de un flujo en movimiento

e=u+Vel²/2+gz    [kJ/kg]

θ= e+PV    [kJ/kg]

θ= u+Vel²/2+gz+PV

θ=h+ Vel²/2+gz    [kJ/kg]

Cantidad de energia transportada

            E_masa=mθ     [kJ]

Tasa de energia transportada

Instrumento	Descripción	Transferencia  de calor	Trabajo	Δep	Δec
Toberas Aceleradoras	incrementa la velocidad de un fluido a expensas de la presión	≈0	0	~=0	≠0
Difusor	incrementa la presión de un fluido al desacelerarlo	≈0	0	~=0	≠0
Turbinas	el fluido pesa por esta y girar la turbina produce trabajo	≈0	EW	~=0	~=0
Compresor	incrementa la presión de un fluido	≈0	EW	~=0	~=0
Válvula de Estrangulamiento	Dispositivo que restringe el fluido con el flujo adiabático		0	~=0	~=0
Cámaras de mezclado	Sección de mezclado de flujos	~=0	0	~=0	~=0
Intercambiadores de calor	Dos corrientes de flujo intercambian calor sin mezclado		0	~=0	~=0

Flujo estacionario

Un difusor de un motor de propulcion entra de forma estacionaria aire a 10ºC y 80kPa con una velocidad de 200m/s. El area de entrada al difusor es 0.4 m². El aire que sale del difusor con una velocidad que es muy pequeña comparada con la velocidad de entrada. Determine

a)      El flujo masico del aire

b)      La temperatura del aire que sale del difusor

parte2